Harmony and Melody
Relationship
How Melody and Harmony relate to each other has been a subject of preoccupation and debate
for over three centuries.
We will present here our concept of this relationship.
Which of the two is the more fundamental?
Is the more fundamental element "born" first?
If so, how is it generated, and how does the other develop from it?
The complete structure of the world of Pitch is involved here.
Definitions
At first we considered the words
"Harmonic", "vertical", and "simultaneous"
as synonymous and interchangeable.
The same applied to the words
"Melodic", "horizontal", and "successive".
The horizontal process of Voice-Leading, within Harmony,
later convinced us that the words "Harmonic" and "Melodic"
should be isolated from the others.
Only recently have we realized that Chord Patterns, especially in Melo-Harmony,
were a succession of vertical events
especially if the Voice-Leading was not specified,
as is the case with chord symbols or with the the harmonic staff.
It seemed high time to rectify this situation with more precise definitions.

1. Harmonic operations are primarily vertical -
the uniform construction of ALL chords, with
the two Primary Notes of the FRAME,
the COMMON TONE and the PROPER TONE, as well as
the two Secondary Notes,
the MEDIAN placed centrally inside the FRAME, and
the MOTRIX placed just outside it,
which not only determines the direction of the chord,
and thus the chord to which it will resolve,
but also the Voice-Leading of the MEDIAN and of the MOTRIX.
2. These Voice-Leading lines are part of Harmony, its horizontal operation,
from which Melody will draw its material.
3. The vertical operations of Harmony also have
their simultaneous elements, each individual chord,
4. as well as
their successive elements, chord patterns.
From a specific chord pattern (at 4),
the Voice-Leading lines (at 2) produce the Basic Materials for the Melody itself.
We have disposed this diagram in such a way as to suggest
the development of the roots of Harmony:
the structure of individual chords, and
the structure of complete chord patterns
with their Voice-Leading possibilities
which in turn serve as roots for Melody.
Chords and Scales
Generation and Just Intonation
The generation of basic materials in the World of Pitch is very intimately associated
with the precise intonation of their distances,
which enables us to generate their structure and preferential (functional) tuning
at the same time, in the same way.
Whether the precision of these distances is preserved or not in performance
does not seem as important as the fact that it was essential to their “birth”.
A musical composition
performed in equi-tempered tuning on a keyboard instrument or
performed in Functional Tuning (Just Intonation) by a choir or an orchestra,
remains essentially the same piece of music, but
Just Intonation played a major, essential part in the “birth” of its basic materials and
equi-tempered tuning had nothing to do with it
(being, above all, a commodity for “fixed pitch” instruments, like keyboards).
This said, it does however seem reasonable, in the performance of a piece of music,
to grant it the tuning of its birth whenever and wherever possible.
Let’s see if we can outline a possibility of “big-bang”
for the generation of basic materials in the World of Pitch.
 |
We will start from the premise (so dear to Einstein)
that nature prefers
the simplest possible mathematical proportions (ratios).
|
How does this apply to distances in the World of Pitch?
 |
- The ratio 1/1 produces exact cloning,
with the interval of the unison.
|
 |
- The ratio 2/1 changes the position of the same note,
with the interval of the octave.
|
The role of the octave is more pertinent and specific
than one might expect at first sight.
Octaves are more "available", and offer more "choice",
in vertical structure than in horizontal structure,
as we will soon see.
 |
- The ratio 3/1 (or more conveniently 3/2 by removing the octave)
is the simplest to generate a truly new note
(actually the only ratio capable of generating all of them),
with the interval of the perfect fifth.
|
It seems impossible to overestimate
the importance of the perfect fifth in the musical language.
It dominates the structure of music completely
and is the source of all its basic materials in the World of Pitch,
including chords and scales.
 |
- the ratio 5/1 (or more conveniently 5/4 by removing the octaves)
plays a secondary role by grafting notes on the series of fifths,
with the interval of the major third, like branches on the trunk of a tree.
|
As we know, the major third which is in Trunk Tuning (Pythagorean), with ratio 81/64
is more complex than that which is in Short Branch Tuning (natural), with ratio 5/4, or 80/64.
Producing a note whose pitch is different
from that of the same note in the series of fifths,
this new ratio of 5/4,
imposing its simplicity in the simultaneous resonance of triads,
will throw a monkey-wrench in the whole process of Just Intonation
and create a complicated process of tuning choices
which we must attempt to decipher.
There seems no point in using more complex ratios (with larger numbers),
the octave, fifth, and major third producing accurate and adequate tuning
for all chordal (vertical) and linear (horizontal) musical situations.
The Generation
|

|
1. The Series of Fifths
We have here 7 adjacent members of the series of fifths,
strung like pearls
within what we call the diatonic Window.
We have not presented the complete series,
with the sharp notes above the Window
and the flat notes below,
merely to save space.
This choice of natural notes is arbitrary,
the most convenient because we have neither sharp nor flat notes,
and we could, with the same results,
have placed the Window in any other key.
Note that we have here 1 set of notes in 1 Window.
Octaves
Each of the seven notes indicated in this diagram
is present at ALL possible octaves.
It would have been preferable to indicate them all
but it would have made the diagram unduly heavy and complicated.
The note "F" is not necessarily lower in pitch than the note "C",
since they are both present at ALL octaves,
and the composer/arranger will have the choice of octave
depending on the circumstances.
This "choice" has occasionally been described as "octave equivalence".
|
|

|
2. Generating diatonic triads
Any two adjacent notes in this series
act as the FRAME of a chord
and the distance of Branch major third has been applied
within each FRAME (either from the top or from the bottom),
dividing it in 2 parts, producing a note (the MEDIAN)
which is already present (with another tuning)
elsewhere in the Window.
Disposition of the triads
We have 3 minor triads in the top of the Window
and 3 major triads in the bottom (in Zarlino tuning).
The minor triads are tuned a comma higher than the major triads.
Note that we have here
2 sets of notes in 1 Window.
Each fifth has been “divided” in 2
by the inserted major third.
Octaves
Once again, each note indicated in this diagram
is present at ALL possible octaves.
In practice, the three notes of a triad
can be placed at any octave,
but the disposition of this diagram is the most useful
to present the generation of triads.
|
|

|
3. Generating diatonic scales
Diatonic scales can be generated by taking the
opposite procedure to the one taken for triads.
Instead of “dividing” each fifth in two,
we shall “multiply” and take every second fifth,
(indicated as a larger note),
in 2 Windows placed, end to end, in a circle.
We have the ratio 9/8 of 2 fifths
for all our major seconds (tones).
It is interesting to note that the 2 minor seconds
(semi-tones), E-F and B-C,
are placed across the lines
where we move into a new window.
Octaves
No question of octave "choice" here -
each note must be at the same octave
as its predecessor, conforming to proximity.
|
Whether the diatonic scale is major, minor, or modal, evidently depends on which note one starts and ends, the tonic (tonal
center) of the scale.
Note that we have here 1 set of notes in 2 Windows
The fifths have been “multiplied” by 2 to produce the major seconds.
4. The Complete Diagram
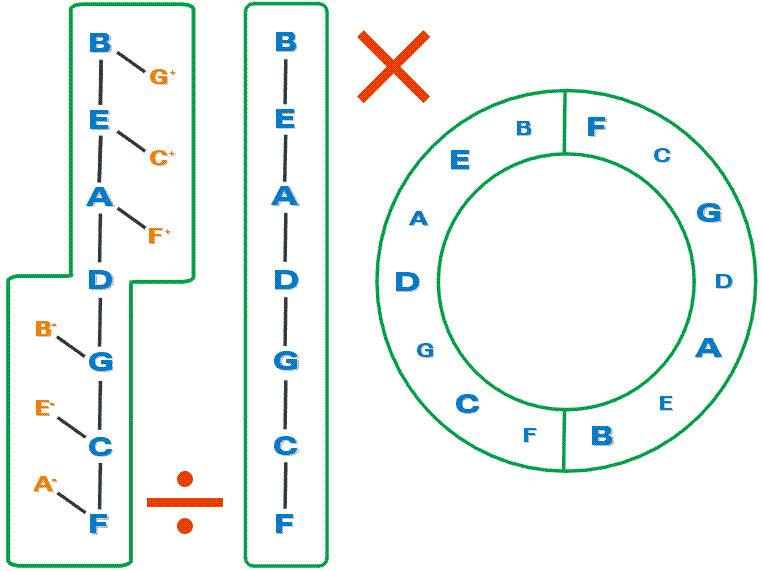
It is interesting to see the 3 diagrams side by side and observe -
1. In the centre, the original series of fifths in the diatonic Window (7 notes)
which acts as generator for both triads and scales.
2. On the left, where the fifths are “divided” by the MEDIAN of each TRIAD,
the major triads (F A- C, C E- G, G B- D) at the bottom, and
the minor triads (D F+ A, A C+ E, E G+ B) at the top;
Triads are part of the basic materials of the chordal structure of Pitch.
3. On the right, the double circle of fifths, where the fifths are “multiplied” by 2,
to produce the scale.
The scale is the basic material of the linear structure of Pitch.
We use the term “circle” of fifths (rather than “series” of fifths)
for evident reasons of dispositon in this diagram.
Definitions
1. A triad can now be defined as
(a) A FRAME consisting of the root and the fifth of the triad, in which
(b) the third has been inserted, and
not 2 thirds superimposed on each other
so that the fifth becomes the result of this addition.
2. A diatonic scale can now be defined as
every second note of the circle of fifths, and
the following example should serve as an efficient illustration of this definition.
Functional Tuning Of The Harmonic Circle
This musical illustration is colored according to the function of each chord component -
COMMON TONE, PROPER TONE, MEDIAN, MOTRIX,
and not according to Trunk Tuning, Short Branch Tuning, and Long Branch Tuning,
The PROPER TONE and the MOTRIX are, generally, in Trunk Tuning.

-Line 5 (the Fundamental Bass) is the circle of fifths itself, in Trunk Tuning,
the original generator, placed in the center of our complete diagram.
Note the relative freedom of octaves here with the alternating fourths and fifths.
Lines 1 and 3 (COMMON TONEs and PROPER TONEs) are Primary Notes of the FRAME,
also in Trunk Tuning, like the scale on the right in the diagram.
The scale in each line uses every second note of the Fundamental Bass.
Everything being in Trunk Tuning there is no tuning conflict
between the “simultaneous resonance” of the triads and
the “successive” tuning of the scale.
Lines 2 and 4 (MEDIANs, and MOTRIXs) are the Secondary Notes,
and involve tuning options which we will discuss
when we have seen the “birth of the MOTRIX" in the Jordan Triangles section.
Note the rigid domination of proximity in these four lines with no "octave choice" whatever.
The MEDIAN is generally in Short Branch Tuning as we saw on the left in the diagram, and
the MOTRIX is generally in Trunk Tuning (as we will later see in Just Intonation).
Line 2 would be tuned E-, E--, D, D, C+, C, B-, C and
Line 4 would be tuned B--, A-, A-, G+, G, F+, F, E-.
On the two first chords, the MOTRIX (major seventh) is in Long Branch Tuning.
On the “buckle” chord, the MEDIAN seems to be in Trunk Tuning
and the MOTRIX seems to be in Short Branch Tuning.
The tuning of Lines 2 and 4, especially for the first 3 Tetrads, may seem unusual,
but it is suggested until we find better.
These two lines (2 and 4) are not pleasantly tuned
when heard successively as a scale,
(with shifts between C+ and C, G+ and G, F+ and F)
and are more suited to the inner (more harmonic) voices.
Lines 1 and 3, on the contrary, are suited to both simultaneous and successive preformance,
and make excellent Soprano lines,
especially Line 1 (degrees 5-4-3-2-1), which we affectionally call “the winner”
because so many melodies end with it (or part of it).
You might like to see the
Jordan Triangles
for another version of the “Big-Bang”.
|


 clips
clips